
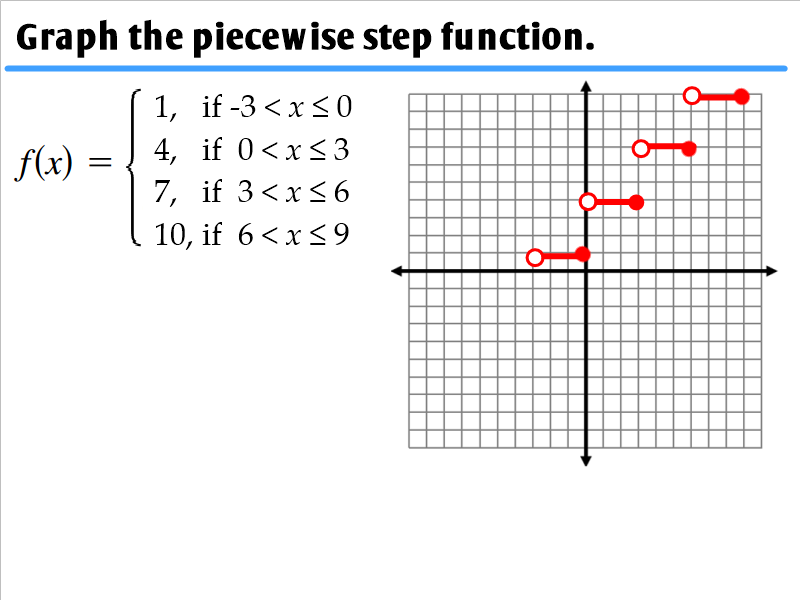
The range is given by U [1, + inf) which is the range of function f. F.IF.C.7: Graphing Piecewise-Defined Functions 3 6 Graph the following piecewise function on the set of axes below.
Be wary of the inequality symbols (<, , >, ) and whether they include.Function f can take only two values: -1 and 2. To graph a piecewise function, graph each subfunction at the indicated domain. The interval (-2, + inf) is open at x = -2 and the graph shows this with an "open point". In the interval (-2, + inf) the graph is a horizontal line y = f(x) = 2 (see formula for this interval above). Notice that the graph in Figure 1 is also the graph of the absolute value function.The absolute value function can therefore also be defined as a piecewise function. Also this interval is closed at x = -2 and therefore the graph must show this : see the "closed point" on the graph at x = -2.
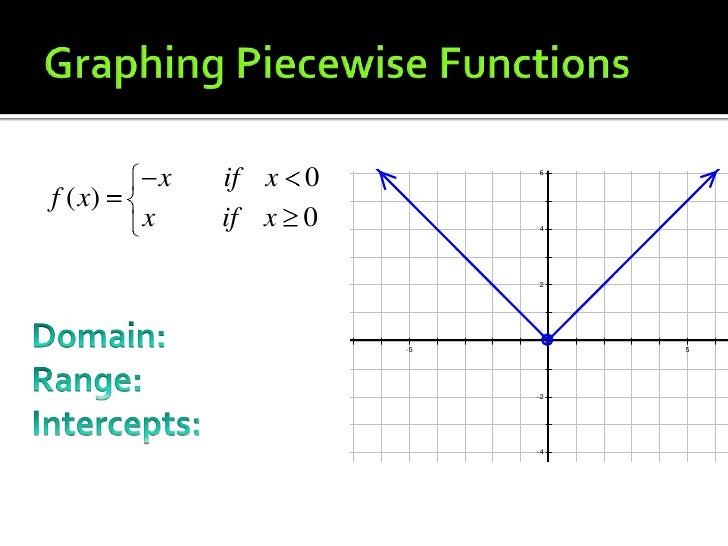
In the interval (- inf, -2] the graph of f is a horizontal line y = f(x) = -1 (see formula for this interval above). We will graph it by considering the value of the function in each interval.
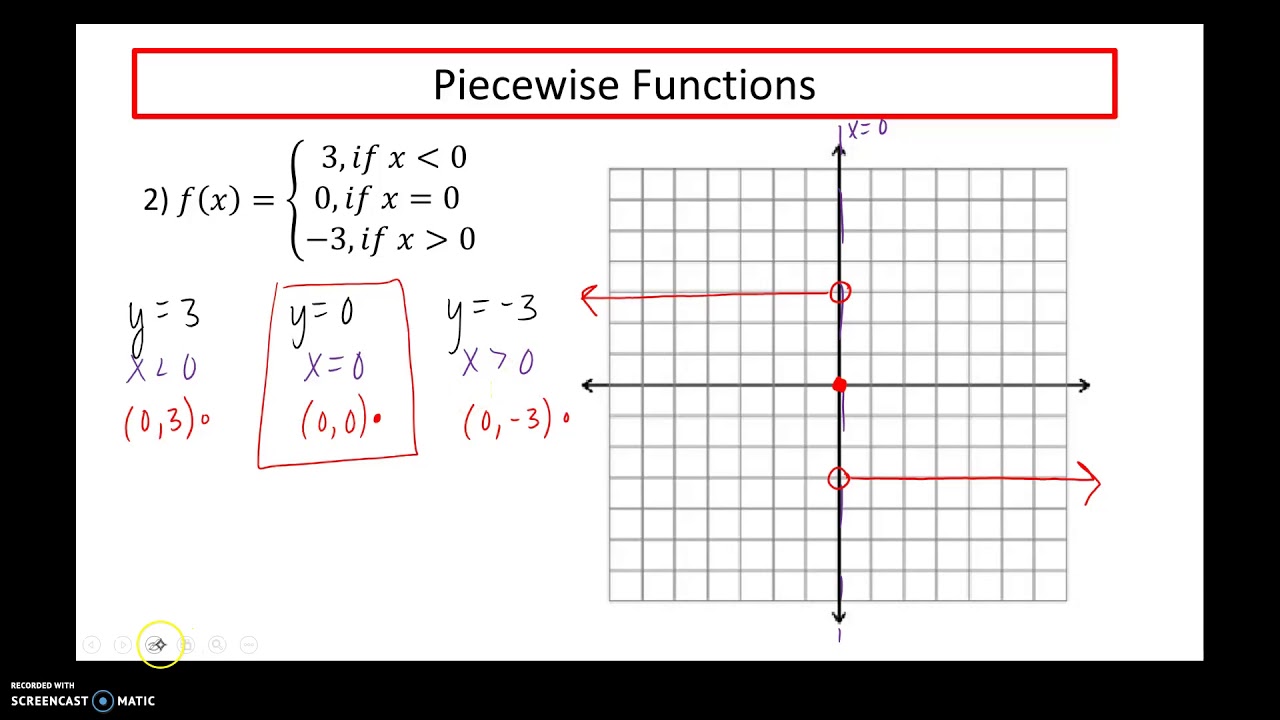
The domain of f is the set of all real numbers. The above function is defined for all real numbers except for values of x in the interval (-2, 2] and x = 4.įind the domain and range of function f and graph it.įunction f is defined for all real values of x. The above function is defined for all real numbers.Īnother example involving more than two intervals. It is also important to note that the domain of function f defined above is the set of all the real numbers since f is defined everywhere for all real numbers. What the above says is that if x is smaller than or equal to 2, the formula for the function is f( x ) = -x and if x is greater than 2, the formula is f( x ) = x.
#Graphing piecewise functions free
Free graph paper is available.Ī piecewise function is usually defined by more than one formula: a fomula for each interval. The graph, domain and range of these functions and other properties are examined. Here we discuss the Methods of using Piecewise Function in Matlab with various statements and examples.A step by step tutorial on graphing and sketching piecewise functions. This is a guide to Piecewise Function in Matlab. And the vectorized approach used in many applications. But, the if-else (loop) approach not used for real-time implementations. As we see above there are three approaches to represent piecewise functions. Piecewise functions are mainly used to represent functions that have various input ranges with different conditions. Matlab programĬonclusion – Piecewise Function in Matlab This shows that x will take the values from – 5 to + 5. Now, as the ranges are known we need to declare the total range of input variable ‘ x’.

In the above example as we know there are two conditions, therefore, we need to define two ranges. Now we will illustrate the above example by using the vectorize approach, First, we need to declare piecewise function like the above examples.Īfter declaring the piecewise function we will define ranges of input variable ‘ x ’. Piecewise Functions Definition, Graph & Examples There are instances where the expression for the functions depends on the given interval of the input values. This is the most popular method in piecewise functions. In this method, the input is the whole vector of sequences(conditions) as well as we can combine two conditions by using ‘ & ’ operator. This method is the second approach of piecewise functions without using loops. The above statements represent ranges of x and respective expected function values. Now inside the switch, there will be different cases, our requirement is only cases so we will write 2 cases. The above statement is the keyword for the switch case for changing values of variable ‘ x’. The above statements show f x is piecewise function concerning input variable ‘ x’, after declaring the function we will start with the switch statement.
To implement the above example by using the switch – case statement first, we need to declare the function statement ( piecewise function). In this example there are two conditions in function f x, one is less than equal to ‘ 0 ’ and the other one is greater than ‘ 0’. it shows that if the value of x is less than or equal to ‘ 0 ’ then out will be ‘ – 2 ’ and if the value of ‘ x ’ is more than ‘ 0 ’ then the output will be ‘ 2’. In above statements if-else statement is used to define the range. In the above statement ‘ f x ’ is the name of the output variable, ‘ piecewise ’ is keyword used for the above function and ‘ x ’ is the input variable.Īfter declaring function now we need to define the conditions of ranges of input variable ‘ x’.


 0 kommentar(er)
0 kommentar(er)
